Just How Secure Is pass-gen?
The other day, I posted on Mastodon that pass-gen (my new passphrase generator written in pure bash and designed to follow the Unix philosophy) has achieved 100 bits of entropy with default settings and is now 128 times as secure as when it first launched. But how secure is 100 bits of entropy, really? And how do you even go about measuring the security of a passphrase generator, really?
Attack Vectors
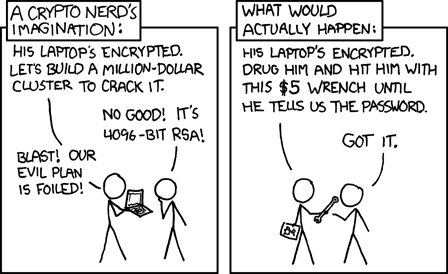
The security of a given password depends entirely on the method used to attack that password. As xkcd famously pointed out, basically all passwords are weak against physical attacks:
But let's set aside the $5-wrench attack for the moment, and dive into the crypto-nerd's imagined attack. Just what would it take to actually crack the sort of password that pass-gen creates?
I'd like to take a look at three attacks and explain why—even with worst-case assumptions, stacking the deck as far as possible in favor of the would-be crackers—pass-gen's passwords would remain secure.
Old-fashioned brute force
The most basic way to crack a password is, of course, to simply try every single possible combination of characters. In theory, this method is guaranteed to work: the cracker will eventually get the correct password if they wait long enough. In practice, little things like impatience, old age, and/or the heat death of the universe tend to get in the way, and this method is rarely successful against any but the most basic of passwords.
Just to sure, though, how would a pass-gen password fare against a brute-force attack? Well, as an example, let's consider this password I just generated:
EMBOSS||comfort||Laborer||HANDLER||powdered||Scarf119
Calculating the difficulty of brute-forcing our password is a simple matter of figuring out how many characters a cracker would need to include to match our password and then raising that number to the power of the length of our password. Here, our password includes lowercase letters (26 possibilities), uppercase letters (26), numbers (10), and special characters (33). So, the full size of the "alphabet" our would-be cracker would need to search would be 95 characters, and they'd be trying to crack a 53-character password. That would be… challenging.
The website password haystacks automates the calculation of just how long this password would take to crack. Here's what it says (with extremely favorable assumptions about the hardware available to the cracker). According to that site, our password would be cracked in: "2.12 billion trillion trillion trillion trillion trillion trillion centuries".
That is about 1,000 times longer than the projected lifespan of the universe, so I think we're safe.
List of known passwords
Of course, a far more common attack is for a cracker to use a list of known passwords. The all-too-often-correct assumption is that people will reuse passwords, and crackers maintain lists billions of past passwords that people have previously used.
The whole point of using a password generator (and then storing the password in a password vault like pass, however, is that you don't reuse passwords. Each password should be used for a single account and for a single account only. If you need to pick a new password, pass-gen makes it easy to do so, and pass (or another password manager) makes it easy to store that password. So just don't reuse passwords, and this attack is no more of a threat than the brute-force attack.
"But," I can already hear you asking, "what if I don't reuse my password, but someone else just happens to have used the same password before?" That is not going to happen. I was going to calculate out the odds of that happening. I was going to imagine that every single one of the 5,115,553,456 passwords in Troy Hunt's Have I Been Pwned
password database had been generated with pass-gen and then calculate the odds of someone else having generated your password.
I was going to do that, but I couldn't find a calculator that would show me an answer other than "0". Suffice it to say, it's just not going to happen.
Dictionary attack
Finally, we're down to the main event: the only strategy that has a prayer of working against a well-designed passphrase.
So, let's start by stacking the deck fully in favor of the cracker: they know that the password was generated with pass-gen. They know that it was generated using the default settings. They know that it was generated from the default word list, rather from any of the dozen+ other wordlists that ship with pass gen.
So, how big is their search space?
Well, given that the pass-gen password is created using a combination of words, symbols and numbers, we can calculate the total number of possible passwords using the following formula:
where w = number of words in our wordlist, p = the number of words we pick for our password, s = the number of symbols on our symbol list, and n = the number of numbers in our password.
That got a bit abstract, so let's go through it with actual numbers. As of today, the default search list includes 8,429 words. However, we effectively have three times that many passwords, because we have three possible capitalization schemes: we pass-gen could produce "example", "Example", or "EXAMPLE"—all three of which are different words for our purposes.
Next, the default configuration chooses 6 of these words for the password. Additionally, pass-gen randomly selects a padding character (or set of two characters) from a list of 54 potential characters, and follows it with a digit between 000 and 999. We can plug those numbers into our formula. Thus, (drumroll please) the total possible number of possible passwords is
Or, put differently, 14 followed by 30 zeros.
Is that a big number? Well, yes, obviously. Ok, better questions: in the context of password security is that a big enough number?
Well, one way security researchers come at that question is to calculate how many bits of entropy the password space generates. That is, what power would we need to raise two to in order to get the large number up above? It turns out that the answer is about 103, so we can say that pass-gen's password has 103 bits of entropy.
There doesn't seem to be a standard recommendation for password entropy, but I'm satisfied that 103 bits is extremely high. I've found recommendations as low as 33 bits, and as high as 80 bits. The EFF Dice passwords—which come from a reputable, paranoid organisation—contain 77 bits of entropy, so I'm inclined to think that anything over that amount is sufficient. (And, recall that the scale is exponential, so entropy of 103 bits doesn't mean that the password is ~25% harder to crack than one with 77 bits of entropy; it means that it is over 67 million times harder to crack.)
Or, circling back to the password haystacks calculator linked above, we can see that a password with 103 bits of entropy would take 35.33 million centuries to crack. That's not exactly heat-death-of-the-universe time, but it's not next Tuesday, either. And recall that the haystacks number assumes extremely* powerful hardware for the potential crackers.
Conclusion
Cutting through the math, the calculations, and the details, the bottom line is clear: if not reused, the passwords generated by pass-gen are secure against any possible cryptographic attack.